В настоящее время нашей стране нужны люди, способные принимать нестандартные решения, умеющие творчески мыслить. Уже давно ученые пытались разгадать загадку творчества и выявили психологические составляющие, необходимые для творческой деятельности. Это:
- гибкость ума, включающая способность к выделению существенных признаков из множества случайных и способность быстро перестраиваться с одной идеи на другую;
- систематичность и последовательность мышления, позволяющая управлять процессами творчества;
- диалектичностъ мышления, при которой мыслящий человек может четко сформулировать противоречие и найти способ его разрешения;
- способность выдвигать гипотезы и уметь их проверять.
Одним из эффективных средств развития творческого мышления являются эвристические задачи. Такие задачи требуют "открыть" (разработать) специфический способ достижения поставленной цели, точно и понятно описать его. Эвристические задачи вовлекают детей в творческую поисковую деятельность, содействуют развитию многих общеинтеллектуальных умений.
Решение эвристических задач требует умения работать с алгоритмами, т.е. планировать последовательность действий для достижения какой-либо цели, а также решать широкий класс задач, для которых ответом является не число или утверждение, а описание последовательности действий.
При творческом подходе к проблеме необходимо выявить новые свойства конкретной ситуации. Особенно важно это при выполнении нестандартных заданий, не имеющих аналогов решения. В таких заданиях сама проблема не всегда четко определена и поэтому нуждается в окончательном формулировании. От решающего требуется умение построить проблемную ситуацию: выделить проблему и критерии оптимального решения.
Задача. Среди трех монет одна фальшивая, она отличается по весу от остальных. Причем неизвестно, легче она или тяжелее. Как с помощью чашечных весов без гирь найти фальшивую монету?
По условию задачи у нас всего три монеты, поэтому положить на чашечку весов можно только по одной монете. Назовем эти монеты "первая" и "вторая" и нарисуем возможные варианты первого взвешивания:
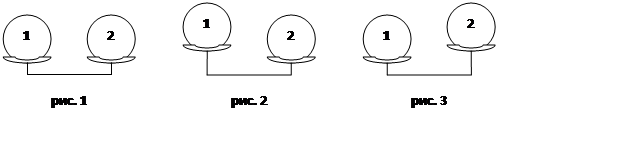
Если весы уравновесились (рис. 1), то первая и вторая монеты одинаковые, т.е. настоящие, значит, фальшивая монета - третья.
Если же весы не уравновесились (рис. 2 и 3), то одна из двух взвешиваемых монет фальшивая, а третья будет точно настоящей, так как фальшивая монета по условию задачи только одна. Чтобы узнать, какая монета из двух фальшивая, надо взвесить одну из "подозреваемых" монет и настоящую. Возможны два варианта выбора монет для взвешивания. Можно взвесить первую монету и третью или вторую и третью. При таких взвешиваниях возможны два результата: весы уравновесятся или нет. Если вес взвешиваемых монет будет равен, значит, фальшивая оставшаяся монета, если нет, то фальшивая - взвешиваемая «подозреваемая» монета.
Ответом этой задачи является разветвляющийся алгоритм. Его можно записать словами, и тогда получится целое сочинение. Такая форма записи очень громоздка и неудобна для анализа. Поэтому в начальных классах можно предложить оформить такой алгоритм в виде блок-схемы. Например:
Больше по теме:
Суть, подходы, цели арт-терапии
Привлекательность метода арт-терапии состоит для современного человека в том, что этот метод в основном использует невербальные способы самовыражения и общения. В процессе творчества активно задействуется правое полушарие мозга. Современн ...
Память человека.
Понятие о памяти в речевом обиходе занимает ведущее место среди всех других психологических терминов. Это в первую очередь связано реальным значением памяти в жизни и деятельности человека. Памяти издревле придавалось большое значение. М ...
Самосожжение женщин в условиях экстремальных психотравмирующих ситуаций
А
нализ современной литературы показывает, что среди различных форм психического реагирования в ответ на комплекс средовых факторов значительноеместо занимает аутоагрессивное поведение [1, 4 – 6].Все возрастающий интерес к проблеме психич ...